Basic algorithm for getting all affected basis functions. More...

#include <GetAffectedBasisFunctions.hpp>

Public Member Functions
	GetAffectedBasisFunctions (GridStorage &storage)

void	operator() (BASIS &basis, const DataVector &point, std::vector< std::pair< size_t, double > > &result)
	Returns evaluations of all basis functions that are non-zero at a given evaluation point. More...

	~GetAffectedBasisFunctions ()

Protected Member Functions
void	rec (BASIS &basis, const DataVector &point, size_t current_dim, double value, GridStorage::grid_iterator &working, index_t *source, std::vector< std::pair< size_t, double > > &result)
	Recursive traversal of the "tree" of basis functions for evaluation, used in operator(). More...

Protected Attributes
GridStorage &	storage

Detailed Description

template<class BASIS>
class sgpp::base::GetAffectedBasisFunctions< BASIS >

Basic algorithm for getting all affected basis functions.

This implicitly assumes a tensor-product approach and local support. No grid points on the border are supported.

The main idea behind this algorithm is to spend as few function evaluations as possible. Assume a regular sparse grid level 3 in two dimensions with the sparse grid basis \(\Phi:=\{\phi_i(x), i=1,\ldots,N\}\). Then the tableau of subspaces looks as follows:

Tableau of subspaces for a regular sparse

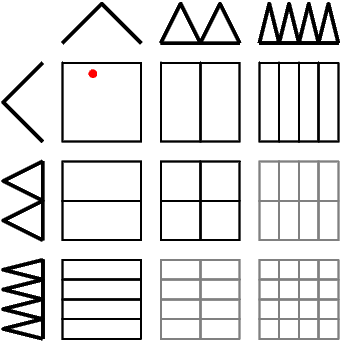
grid level 3" You could evaluate the function \( f_N(x) = \sum_{i=1}^N \alpha_i \phi_i(x)\) for all basis functions \(\phi_i(x)\), multiply them with the surplus and add them up. In \(d\) dimensions this would lead to \(N\) evaluations of \(d\) one-dimensional basis functions each.

A better way is to (recursively) look at each subspace, as only one basis function per subspace can be non-zero (partially disjunct supports):

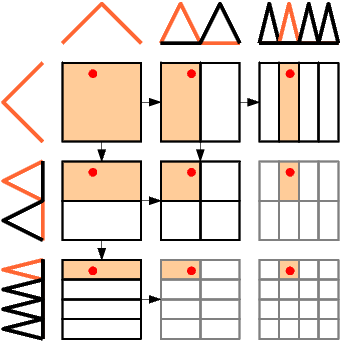
GetAffectedBasisFunctions_subspaces_affectedBasisFunctions.png

Traversal of

subspaces for evaluation" This can be done recursively in both the dimension and the level. In each subspace the basis function concerned can be identified via a few index calculations and evaluated at the given point in the domain.

Even better would be to save further function evaluations and to reuse intermediate values obtained by the evaluation of one-dimensional basis functions, see the following figure.

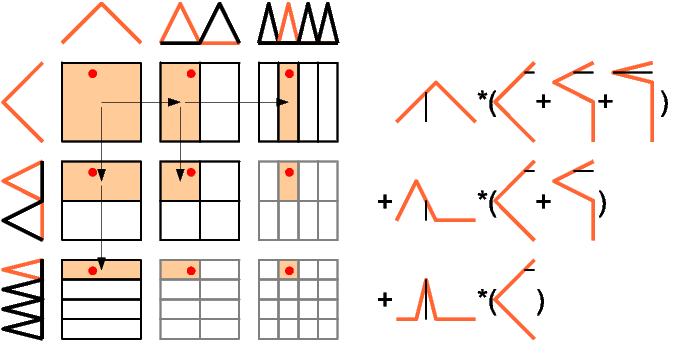
GetAffectedBasisFunctions_subspaces_affectedBasisFunctions_recursive.png

Minimize

the number of evaluations" width=10cm Descending recursively in the d-th dimension, one can propagate the value of the intermediate function evaluation for the first d-1 dimensions that have already been looked at.

Constructor & Destructor Documentation

◆ GetAffectedBasisFunctions()

template<class BASIS>

sgpp::base::GetAffectedBasisFunctions< BASIS >::GetAffectedBasisFunctions ( GridStorage & storage )

inlineexplicit

◆ ~GetAffectedBasisFunctions()

template<class BASIS>

sgpp::base::GetAffectedBasisFunctions< BASIS >::~GetAffectedBasisFunctions ( )

inline

Member Function Documentation

◆ operator()()

template<class BASIS>

void sgpp::base::GetAffectedBasisFunctions< BASIS >::operator()	(	BASIS &	basis,
		const DataVector &	point,
		std::vector< std::pair< size_t, double > > &	result
	)

inline

Returns evaluations of all basis functions that are non-zero at a given evaluation point.

For a given evaluation point \(x\), it stores tuples (std::pair) of \((i,\phi_i(x))\) in the result vector for all basis functions that are non-zero. If one wants to evaluate \(f_N(x)\), one only has to compute

\[ \sum_{r\in\mathbf{result}} \alpha[r\rightarrow\mathbf{first}] \cdot r\rightarrow\mathbf{second}. \]

Parameters

basis	a sparse grid basis
point	evaluation point within the domain
result	a vector to store the results in

References chess::dim, sgpp::base::HashGridStorage::getDimension(), sgpp::base::GetAffectedBasisFunctions< BASIS >::rec(), and sgpp::base::GetAffectedBasisFunctions< BASIS >::storage.

◆ rec()

template<class BASIS>

void sgpp::base::GetAffectedBasisFunctions< BASIS >::rec	(	BASIS &	basis,
		const DataVector &	point,
		size_t	current_dim,
		double	value,
		GridStorage::grid_iterator &	working,
		index_t *	source,
		std::vector< std::pair< size_t, double > > &	result
	)

inlineprotected

Recursive traversal of the "tree" of basis functions for evaluation, used in operator().

For a given evaluation point \(x\), it stores tuples (std::pair) of \((i,\phi_i(x))\) in the result vector for all basis functions that are non-zero.

Parameters

basis	a sparse grid basis
point	evaluation point within the domain
current_dim	the dimension currently looked at (recursion parameter)
value	the value of the evaluation of the current basis function up to (excluding) dimension current_dim (product of the evaluations of the one-dimensional ones)
working	iterator working on the GridStorage of the basis
source	array of indices for each dimension (identifying the indices of the current grid point)
result	a vector to store the results in