sgpp::base::ConvertLinearToPrewavelet Class Reference

Class that implements the transformation of a hierarchical linear sparse grid to a hierarchical prewavelet sparse grid. More...

#include <ConvertLinearToPrewavelet.hpp>

Public Member Functions
	ConvertLinearToPrewavelet (GridStorage &storage, GridStorage &shadowstorage)
	Constructor, must be bind to a grid. More...
void	operator() (DataVector &source, DataVector &result, grid_iterator &index, size_t dim)
	Converts a given linear base to a prewavelet base. More...
	~ConvertLinearToPrewavelet ()
	Destructor. More...

Protected Types
typedef GridStorage::grid_iterator	grid_iterator
typedef index_t	index_type
typedef level_t	level_type

Protected Attributes
GridStorage &	shadowstorage
GridStorage &	storage
	the grid object More...

Detailed Description

Class that implements the transformation of a hierarchical linear sparse grid to a hierarchical prewavelet sparse grid.

Therefore the ()operator is implemented in order to use the sweep algorithm for the grid traversal. Let the coefficients from the hat basis be \( h_{l,i}\) and from the prewavelet basis \( u_{l,i} \). To calculate the surplusses, temp values are needed:

\[ (l,i)\neq G_{n}^{1}:t_{l,i}=-\frac{6}{10}u_{l,i\pm1}+t_{l+1,2i} \]

All temp values for levels greater than the maximal level of the grid are set to 0. The actual transformation is defined by the following tridiagonal equation system:

\begin{eqnarray*} \frac{16}{10}u_{l,i}+\frac{4}{10}u_{l,i\pm2}&=&h_{l,i}-t_{l+1,2i}+\frac{1}{2}t_{l+1,2(i\pm1)}\\\frac{12}{10}u_{l,1}+\frac{4}{10}u_{l,3}&=&h_{l,1}-t_{l+1,2}+\frac{1}{2}t_{l+1,4}\\\frac{12}{10}u_{l,2^{l}-1}+\frac{4}{10}u_{l,2^{l}-3}&=&h_{l,2^{l}-1}-t_{l+1,2(2^{l}-1)}+\frac{1}{2}t_{l+1,2(2^{l}-2)} \end{eqnarray*}

For solving these tridiagonal systems, the method described in http://www.nrbook.com/a/bookcpdf/c2-4.pdf was used. Some odd Fileopen® plugin is needed to open that file ... sorry for that! the picture depicts all needed variables in oder to perform the transformation:

This picture shows all involved gridpoints (red crosses) and temp values (green circles) to calculate the new hierarchical coefficients (red arrows) and new temp values (green arrows).

Member Typedef Documentation

grid_iterator

typedef GridStorage::grid_iterator sgpp::base::ConvertLinearToPrewavelet::grid_iterator

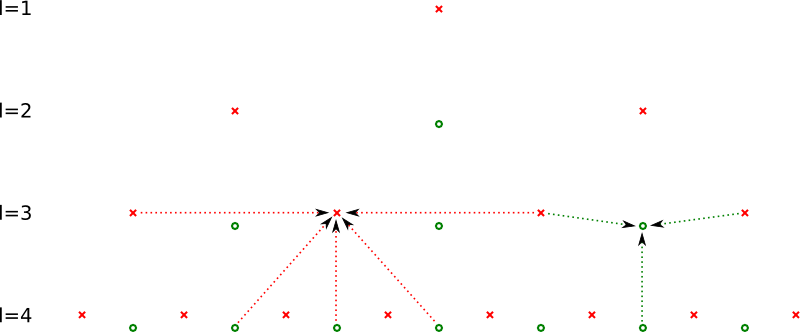
protected

index_type

typedef index_t sgpp::base::ConvertLinearToPrewavelet::index_type

protected

level_type

typedef level_t sgpp::base::ConvertLinearToPrewavelet::level_type

protected

Constructor & Destructor Documentation

ConvertLinearToPrewavelet()

sgpp::base::ConvertLinearToPrewavelet::ConvertLinearToPrewavelet ( GridStorage &  storage, GridStorage &  shadowstorage  )

inline

Constructor, must be bind to a grid.

An adaptive grid with prewavelet ansatz functions requires for operations using the up-down algorithm shadow points. These shadow points a needed just for data transport, thus they do not have an influence on the final function. Please refer to sgpp::pde::UpDownOneOpDimWithShadow for more information.

Parameters

storage	the grid storage object of the the grid, on which the hierarchisation should be executed
shadowstorage	shadow points (see detailed description)

~ConvertLinearToPrewavelet()

sgpp::base::ConvertLinearToPrewavelet::~ConvertLinearToPrewavelet ( )

inline

Destructor.

References chess::dim, and operator()().

Member Function Documentation

operator()()

void sgpp::base::ConvertLinearToPrewavelet::operator()	(	DataVector &	source,
		DataVector &	result,
		grid_iterator &	index,
		size_t	dim
	)

Converts a given linear base to a prewavelet base.

References sgpp::base::HashGridIterator::get(), sgpp::base::HashGridIterator::getGridDepth(), python.statsfileInfo::i, sgpp::base::HashGridStorage::isInvalidSequenceNumber(), level, chess::r, sgpp::base::HashGridIterator::seq(), sgpp::base::HashGridIterator::set(), storage, and python.utils.pca_normalize_dataset::u.

Referenced by ~ConvertLinearToPrewavelet().

Member Data Documentation

shadowstorage

GridStorage& sgpp::base::ConvertLinearToPrewavelet::shadowstorage

protected

storage

GridStorage& sgpp::base::ConvertLinearToPrewavelet::storage

protected

the grid object

Referenced by operator()().

---

The documentation for this class was generated from the following files:

• base/src/sgpp/base/operation/hash/common/algorithm_sweep/ConvertLinearToPrewavelet.hpp
• base/src/sgpp/base/operation/hash/common/algorithm_sweep/ConvertLinearToPrewavelet.cpp