sgpp::pde::LaplaceDownGradientPrewavelet Class Reference

Implements the downGradient Method needed for the Laplace operator on prewavelet grids. More...

#include <LaplaceDownGradientPrewavelet.hpp>

Public Member Functions
	LaplaceDownGradientPrewavelet (sgpp::base::GridStorage *storage)
	Constructor. More...
void	operator() (sgpp::base::DataVector &source, sgpp::base::DataVector &result, grid_iterator &index, size_t dim)
	This operations performs the calculation of downGradient in the direction of dimension dim More...
	~LaplaceDownGradientPrewavelet ()
	Destructor. More...

Protected Types
typedef sgpp::base::GridStorage::grid_iterator	grid_iterator

Protected Attributes
sgpp::base::GridStorage *	storage
	Pointer to sgpp::base::GridStorage object. More...

Detailed Description

Implements the downGradient Method needed for the Laplace operator on prewavelet grids.

The calculation is done iterative and utilizes the following temp variables:

\begin{eqnarray*} t_{k,j}&=&\frac{1}{h_{k}}\left(\frac{32}{10}u_{k,j}+\frac{8}{10}u_{k,j\pm2}\right) \quad(k,j)\in G_{n}^{1}\\ t_{k,j}&=&\frac{1}{h_{k}}\left(\frac{24}{10}u_{k,j}+\frac{8}{10}u_{k,j\pm2}\right) \quad(k,j)\in G_{n}^{1}\mbox{ and next to border}\\ t_{k,j}&=&t_{k-1,\frac{j}{2}}-\frac{1}{h_{k}}\left(\frac{23}{10}u_{k,j\pm1}+\frac{1}{10}u_{k,j\pm3}\right) \quad(k,j)\notin G_{n}^{1}\\ t_{k,j}&=&t_{k-1,\frac{j}{2}}-\frac{1}{h_{k}}\left(\frac{22}{10}u_{k,j\pm1}+\frac{1}{10}u_{k,j\pm3}\right) \quad(k,j)\notin G_{n}^{1}\mbox{ and \ensuremath{(k,j\pm1)}next to border} \end{eqnarray*}

The calculation of the results is as follows:

\begin{eqnarray*} r_{k,j}&=&-\frac{6}{10}t_{k-1,\frac{j\pm1}{2}}\\ &&+\frac{1}{h_{k}}u_{k,j}\cdot\left[\frac{612}{100}\mbox{ if \ensuremath{(k,j)} inner point, or } \frac{356}{100}\mbox{ if \ensuremath{(k,j)} border point}\right]\\ &&+\frac{1}{h_{k}}u_{k,j\pm2}\cdot\left[\frac{256}{100} \mbox{ if \ensuremath{(k,j)} and \ensuremath{(k,j\pm2)} inner point, or } \frac{242}{100} \mbox{ if \ensuremath{(k,j)} or \ensuremath{(k,j\pm2)} border point, or } \frac{228}{100} \mbox{ if \ensuremath{(k,j)} border point}\right]\\ &&+\frac{1}{h_{k}}u_{k,j\pm4}\cdot\frac{14}{100}\\r_{1,1}&=&4u_{1,1} \end{eqnarray*}

Please note, that all values of gridpoints outside of the sparse grid are treated as 0. The following picture depicts all involved grid points and temp values in order to calculate a specific point:

All involved gridpoint for the up algorithm (red) and temp

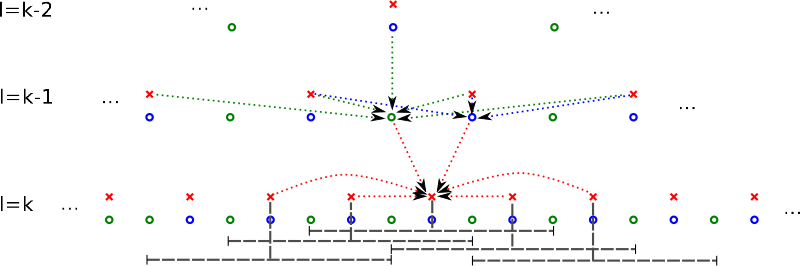
points between grid points (green). The gray line indicates the support of the prewavelet."

Member Typedef Documentation

grid_iterator

typedef sgpp::base::GridStorage::grid_iterator sgpp::pde::LaplaceDownGradientPrewavelet::grid_iterator

protected

Constructor & Destructor Documentation

LaplaceDownGradientPrewavelet()

sgpp::pde::LaplaceDownGradientPrewavelet::LaplaceDownGradientPrewavelet ( sgpp::base::GridStorage *  storage )

explicit

Constructor.

Parameters

storage

the grid's sgpp::base::GridStorage object

~LaplaceDownGradientPrewavelet()

sgpp::pde::LaplaceDownGradientPrewavelet::~LaplaceDownGradientPrewavelet

(

)

Destructor.

Member Function Documentation

operator()()

void sgpp::pde::LaplaceDownGradientPrewavelet::operator()	(	sgpp::base::DataVector &	source,
		sgpp::base::DataVector &	result,
		grid_iterator &	index,
		size_t	dim
	)

This operations performs the calculation of downGradient in the direction of dimension dim

Parameters

source	sgpp::base::DataVector that contains the gridpoint's coefficients (values from the vector of the laplace operation)
result	sgpp::base::DataVector that contains the result of the down operation
index	a iterator object of the grid
dim	current fixed dimension of the 'execution direction'

References sgpp::base::HashGridIterator::get(), sgpp::base::HashGridIterator::getGridDepth(), h, python.statsfileInfo::i, sgpp::base::HashGridStorage::isInvalidSequenceNumber(), sgpp::base::HashGridIterator::leftChild(), sgpp::base::HashGridIterator::seq(), sgpp::base::HashGridIterator::set(), sgpp::base::HashGridIterator::stepRight(), and storage.

Member Data Documentation

storage

sgpp::base::GridStorage* sgpp::pde::LaplaceDownGradientPrewavelet::storage

protected

Pointer to sgpp::base::GridStorage object.

Referenced by operator()().

---

The documentation for this class was generated from the following files:

• pde/src/sgpp/pde/basis/prewavelet/algorithm_sweep/LaplaceDownGradientPrewavelet.hpp
• pde/src/sgpp/pde/basis/prewavelet/algorithm_sweep/LaplaceDownGradientPrewavelet.cpp