sgpp::base::PrewaveletBasis< LT, IT > Class Template Reference

Class representing a prewavelet base. More...

#include <PrewaveletBasis.hpp>

Inheritance diagram for sgpp::base::PrewaveletBasis< LT, IT >:

Public Member Functions
double	eval (LT level, IT index, double p) override
	Evaluate a basis function. More...
size_t	getDegree () const override
	Returns the polynomial degree of the basis. More...
double	getIntegral (LT level, IT index) override
	returns the integal of the current basis function More...
	~PrewaveletBasis () override
	Destructor. More...
Public Member Functions inherited from sgpp::base::Basis< LT, IT >
virtual	~Basis ()
	Destructor. More...

Detailed Description

template<class LT, class IT>
class sgpp::base::PrewaveletBasis< LT, IT >

Class representing a prewavelet base.

A prewavelet \(\psi\) is a combination of 5 normal hat functions \(\phi\) with a \(\left[\frac{1}{10}, -\frac{6}{10}, 1, -\frac{6}{10}, \frac{1}{10}\right]\) stamp:

\[ \psi_{(l,i)} = \frac{1}{10}\phi_{(l,i-2)} - \frac{6}{10}\phi_{(l,i-1)} + \phi_{(l,i)} - \frac{6}{10} \phi_{(l,i+1)} + \frac{1}{10}\phi_{(l,i+2)} \]

Next to the border:

\[ \psi_{(l,1)} = \frac{9}{10}\phi_{(l,1)} - \frac{6}{10}\phi_{(l,2)} + \frac{1}{10}\phi_{(l,3)} \]

For level \( l = 1\) the prewavelet and linear basis are equivalent.

Normal prewavelet base function and a left border prewavelet. The

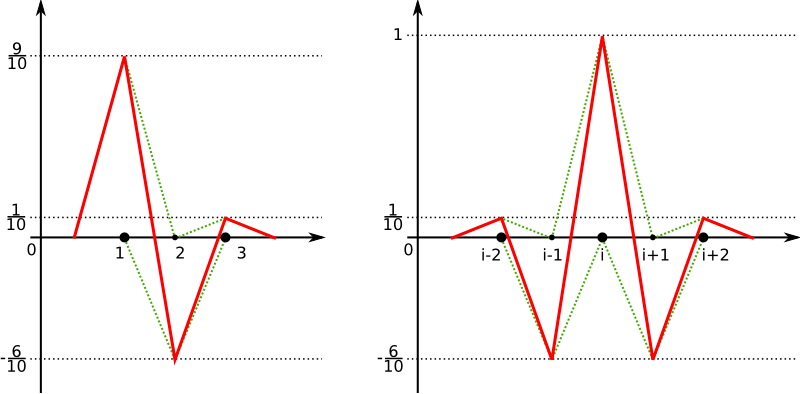
bold dots indicate the position of other prewavelet basis functions on the same level, the thin dots representing grid points missing in the sparse grid on that level. Please note that the left and right TWO neighbors are interfering with a specific prewavelet base." The prewavelets form a semi-orthogonal basis. That means \(<\psi_{(i,l)},\psi_{(j,k)}> = 0\) if \(l\neq k\). On the same level, the prewavelets are not orthogonal. This property will ease the calculation of some specific operations, but on the other hand, this advantage is bought with a wider support of the ansatzfunctions.

Constructor & Destructor Documentation

~PrewaveletBasis()

template<class LT, class IT>

sgpp::base::PrewaveletBasis< LT, IT >::~PrewaveletBasis ( )

inlineoverride

Destructor.

Member Function Documentation

eval()

template<class LT, class IT>

double sgpp::base::PrewaveletBasis< LT, IT >::eval ( LT  level, IT  index, double  p  )

inlineoverridevirtual

Evaluate a basis function.

Has a dependence on the absolute position of grid point and support.

Implements sgpp::base::Basis< LT, IT >.

References level.

Referenced by python.uq.analysis.asgc.ASGCAnalysis.ASGCAnalysis::estimateDensity(), and sgpp::base::GetAffectedBasisFunctions< PrewaveletBasis< unsigned int, unsigned int > >::rec().

getDegree()

template<class LT, class IT>

size_t sgpp::base::PrewaveletBasis< LT, IT >::getDegree ( ) const

inlineoverridevirtual

Returns the polynomial degree of the basis.

Returns

polynomial degree of the basis

Implements sgpp::base::Basis< LT, IT >.

getIntegral()

template<class LT, class IT>

double sgpp::base::PrewaveletBasis< LT, IT >::getIntegral ( LT  level, IT  index  )

inlineoverridevirtual

returns the integal of the current basis function

Parameters

level	level of the basis function
index	index of the basis function

Returns

Implements sgpp::base::Basis< LT, IT >.

---

The documentation for this class was generated from the following file:

• base/src/sgpp/base/operation/hash/common/basis/PrewaveletBasis.hpp